Dzisiaj, w dzień wolny od zajęć w szkole, proponujemy lekturę, ostrzegamy –  niekrótkiego tekstu, który zaczerpnęliśmy, bez skrótów, z fejsbukowego profilu szachisty, ale i eksperta w temacie matematyki – Tomasza Pintala. Jesteśmy przekonani, że powinien on zaciekawić, i dać dużo do myślenia, nie tylko nauczycieli, nauczających w szkołach matematyki:

 

 

 

A teraz nasz Tomasz wyjaśni dlaczego treści abstrakcyjne powinny być realizowane dopiero w szkole średniej i jaki jest sens rozciągać treści konkretne do końca szkoły podstawowej.

 

>Ktoś jest gotowy? Mam już słuchaczy na widowni? A może gdzieś w ciepłym łóżeczku czy też kanapie a może i w fotelu? Tak czy inaczej już wyjaśniam, bo to kolejny klocek w całej tej układance, którą wspólnie układamy kochani. Matematyka naprawdę może być piękna i wartościowa, a edukacja matematyczna może być o niebo lepsza. Tak, dobrze czytacie – o niebo lepsza, bo to co obecnie realizujemy pod hasłem „matematyczna edukacja” to jest po prostu jakieś grube NIEPOROZUMIENIE i przy okazji niezrozumienie oraz ignorancja jeśli chodzi o badania naukowe związane z tym czym jest nauka, edukacja, matematyka, mózg i tego typu kwestie.

 

>To lecimy, bo dziś będzie grubo. A przynajmniej ja tak to widzę. Gwarantuję, że jeśli uważnie przeczytacie to co dziś chcę przekazać i zrozumiecie ideę, która za tym stoi, to oczy po raz kolejny wyjdą wam z orbit. Chyba, że jesteście ekspertami, to wtedy nie, ale wówczas będziecie mieli potwierdzenie, że pracujecie jak najbardziej prawidłowo!

 

>Otóż w szkole podstawowej obecnie jest za dużo treści do realizacji oraz część jest na poziomie abstrakcyjnym, co nie ma sensu jeśli mówimy o bardzo efektywnej nauce. A jak jeszcze realizujemy treści wymagające abstrakcyjnego myślenia, gdy ono się jeszcze nie rozwinęło, to przepalamy kasę… wróć! przepalamy cenne godziny prawdziwej matematycznej edukacji

 

>Jaki zatem mam pomysł, aby owa edukacja miała nie tylko ręce i nogi, ale żeby była „jak (najlepsza) książka pisze”?

 

1.Treści abstrakcyjne przechodzą do klasy 1 szkoły średniej. Inaczej mówiąc, są realizowane dopiero wtedy gdy mózg jest już na to w pełni gotowy u każdego dziecka (ucznia).

 

2.Przez całą szkołę podstawową realizujemy wszystkie zagadnienia, które są i mogą być realizowane na konkretach.

 

3.Tradycyjnie ostatnie 2 lata szkoły podstawowej (czyli klasa 7 i 8 SP) w których były (nadal są) realizowane treści o charakterze myślenia abstrakcyjnego, są zamieniane na znaczne bogatsze omówienie i przećwiczenie zagadnień o charakterze myślenia konkretnego.

 

4.Dzięki temu zrealizujemy więcej treści na znacznie głębszym poziomie i będzie mniejsza szansa na to, że uczniowie „zdążą” nabawić się tak zwanych zaległości, które potem im bardzo mocno hamują i niekiedy uniemożliwiają dalszą efektywną edukację matematyczną.

 

5.Zagadnienia matematyczne realizujemy w taki sposób, aby każde dziecko mogło jak najwięcej odkrywać oraz manipulować na konkretach. Teoria dopiero wtedy jest formułowana i zapisywana, gdy proces odkrywania przynosi konkretne efekty.

 

6.Każde dziecko może dochodzić do istotnych wniosków na swój indywidualny sposób. Zadaniem mistrza jest sprawdzenie oraz ocena poprawności procesu oraz końcowych wniosków. Inaczej mówiąc, chodzi o to czy nie ma błędów logicznych i czy rozumowanie jest spójne, poprawne oraz wynikowe.

 

7.Nauczyciel tworzy dzieciom warunki do tworzenia, odkrywania, testowania jak i dzielenia się swoimi doświadczeniami oraz wnioskami z innymi dziećmi. W zależności od możliwości są one w formie pracy indywidualnej, grupowej, projektowej oraz takich w których proces edukacyjny w danej grupie dzieci daje najlepsze efekty.

 

No i jak kochani? Grubo nie? Tak, wiem, wiem. Teraz mam pokazać na wybranym przykładzie jak to zrobić i wyjaśnić dlaczego tak a nie inaczej oraz podkreślić pozytywne i długotrwałe efekty mojego podejścia.

 

Zatem zaczynajmy.

 

–Pamiętacie może taki temat jak TWIERDZENIE PITAGORASA?

 

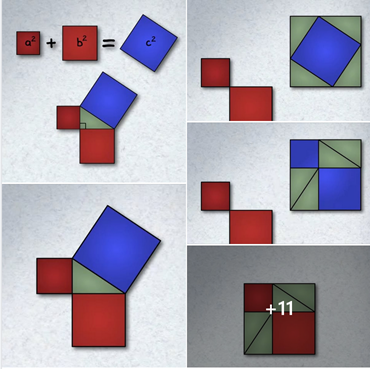
-Tak, to jest ten temat, w którym mamy trójkąt prostokątny, a na bokach każdego z nich rysujemy kwadraty i potem jak dodamy pola tych dwóch „mniejszych” kwadratów, to będzie ono równe polu „największego” kwadratu.

 

 

–Zerknijcie na pierwszy obrazek (slajd) a natychmiast wszystko stanie się jasne. Jak możecie na razie nie patrzcie na kolejne (chyba, że ciekawość was pokona), bo w ten sposób lepiej zrozumiecie mój pomysł i jego głębię. Tak naprawdę to są dość oczywiste rzeczy, ale dla osób, które tym się nie zajmują zawodowo, mogą one być zupełnie niewidoczne. Nie martwcie się jednak, przecież powiedziałem, że wyjaśnię i pomogę zrozumieć, prawda? No właśnie!

 

–Teraz będę zadawał wam trudne pytania, które chciałbym abyście odbierali dwutorowo. Pierwszy tor to pytanie do was bezpośrednio, a drugi tor – to samo pytanie, ale do „waszego dziecka”. I to nie ma zanaczenia czy to wasze w sensie urodzone lub wychowywane przez was dziecko czy też takie, które dobrze znacie – ważne, aby wyobrazić sobie tę sytuację i ją porównać.

 

TRUDNE PYTANIA DO WAS i/lub DO WASZYCH DZIECI

 

-Pytanie nr 1: Czy rysowaliście w zeszycie ten pełny rysunek? (3 kwadraty na wszystkich bokach trójkąta równobocznego)

 

-Pytanie nr 2: Czy kolorowaliście każdy z kwadratów innym kolorem? Czy był wyjaśniony sens użycia różnych kolorów?

 

-Pytanie nr 3: Czy rysowaliście identyczne kwadraty, ale bez trójkąta, lecz jeden obok drugiego w kontekście równania (A + B = C, a u nas byłoby to A^2 + B^2 = C^2) – ponownie: proszę, abyście zerknęli na obrazek nr 1

 

-Pytanie nr 4: Czy dyskutowaliście na lekcji ze sobą w parach a później z nauczycielem o tym dlaczego tak się dzieje? Czemu te pola dwóch mniejszych kwadratów są równe temu największemu?

 

-Pytanie nr 5: Czy każdy z was samodzielnie wycinał oraz rozcinał na kartce poszczególne części tych kwadratów, układając je w największy kwadrat?

 

-Pytanie nr 6: Na ile sposobów rozcinaliście te kwadraty, aby sprawdzić czy się na siebie będą idealnie nakładać (pokrywać)?

 

-Pytanie nr 7: Czy w procesie wycinania i rozcinania, nauczyciel powiedział lub pokazwał wam jak je można (należy) rozcinać, tak aby wszystkie części idealnie się pokrywały?

 

-Pytanie nr 8: Który z podanych przez nauczyciela sposobów sprawdziliście i który wybraliście jako najbardziej przemawiający do was? Czy był to jeden sposób czy więcej?

 

-Pytanie nr 9: Czy ktoś z was wpadł na pomysł, aby zapytać czy inne figury oprócz kwadratów również mają tę właściwość? Czy może nauczyciel wspomniał, że na bokach trójkąta prostokątnego mogą być dowolne wielokaty formne czy też półkola, a dalej wzór działa poprawnia?

 

-Pytanie nr 10: Czy mieliście okazję przetestować tę koncepcję na przykładzie pomocy naukowej w której kręcicie korbą, a woda która jest w tych dwóch mniejszych kwadratach przelewa się (w całości) do tego największego, a potem na odwrót?

 

 

W tym momencie mógłbym podziękować wam za uwagę oraz zamknąć wirtualną aulę i oddać klucz na portiernię, prawda? Pozamiatane?

 

Teraz ważna uwaga: w tym momencie mogą się u was pojawić emocje lub wspomnienia związane z tym, że coś was ominęło czy też złość albo smutek odnośnie tego, że nie mieliście okazji ku temu, żeby tego samemu doświadczyć. To niestety „normalne”, bo tego eksperymentu oraz koncepcji nie doświadcza jakieś 90-95% uczniów. Poprzez normalne mam na myśli tutaj znaczenie „powszechne” a nie pożądane.

 

>A teraz zastanówcie się kochani nad tym, ile zadań robiliście na lekcji oraz ile musieliście zrobić w domu oraz na sprawdzianach, w których liczyliście te pola kwadratów albo długości boków trójkąta? A jak dołożymy jeszcze pierwiastki, to czy każdy z was dobrze je rozumiał?

 

–Widzicie co się tutaj dzieje? Młodzież by powiedziała, że to albo „naprawdę niezła jazda” albo znacznie mocniej „co się tutaj odwaliło?”.

 

–A teraz zastanówmy się ile obliczeń wymagało zrealizowanie poleceń, które zawarłem w pytaniach od 1 do 10. Zauważyliście, że to wszystko było i jest praca na konkretach? Widzicie, że pytania nr 9 i 10 można przenieść na kolejne zajęcia i je zrealizować także z kolejnymi (innymi) jako takie przypomnienie i poszerzenie?

 

–Dalej. Jeśli mamy wielokrotność 5 uczniów, powiedzmy klasa 20 lub 25 dzieci, to jak podamy im możliwość sprawdzenia na 5 sposobów, to jest ogromna szansa na to, że każdy z nich będzie miał swój sposób, a jak będą chcieli sprawdzić pozostałe, to raz że mogą to zrobić albo w wolnym czasie bądź też każda grupa prezentuje jeden sposób tego udowodnienia, a pozostali patrzą, słuchają, zadają pytania i jednocześnie wykonują razem z grupą ekspertów.

 

–No i dochodzimy do kluczowej kwestii. Jak myślicie kochani ile jest sposobów na to, aby udowodnić twierdzenie Pitagorasa? Dodam, że w naszym przykładzie posługujemy się wyłącznie tak zwanymi dowodami wizualnymi (visual proofs), ponieważ one mogą być bez problemu zrealizowane właśnie poprzez manipulacje na konkretach. A gdyby tak wziąć pod uwagę jeszcze wszystkie te, które są dowodzone na poziomie myślenia abstrakcyjnego? Ile by ich w sumie było? Spróbujcie się chwilę zastanowić i zapiszcie swoją liczbę.

 

–Takich sposobów na udowodnienie twierdzenia Pitagorasa jest uwaga…. CO NAJMNIEJ 367! Tak, prawie 400 sposobów na to, żeby przekonać się o tym, że prawdą jest twierdzenie, które jest formułowane w podręcznikach jako: „Jeśli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej” (Matemaks).

 

>A jak zapytamy dzieci, aby same sformułowały? To jak wtedy to będzie? W zależności od dojrzałości, doświadczenia oraz umiejętności werbalnych będzie to coś w rodzaju:

 

-„Jak narysujemy te kwadraty na tych bokach przy kącie prostym, to będą miały razem takie samo pole jak ten kwadrat narysowany na najdłuższym boku„. Czy jest to poprawne? Absolutnie tak!

 

-Potem możemy dodać, że te boki przy kącie prostym to tak zwane przyprostokątne, zaś ten naprzeciwko – przeciwprostokątna. I wszystko jest gites, cacy i elegancko!

 

-Teraz zobaczcie kochani, że gdybyśmy uczyli poprzez odkrywanie oraz tworzyli warunki dzieciom do tego, aby to odkrywanie było znacznie bardziej efektywne, to ich poziom kompetencji matematycznych byłby taki, że głowa mała: mózg staje, głowa boli!

 

–Katowanie ich niezrozumiałymi dla nich nazwami, pojęciami oraz zmuszanie do rozwiązywania zadań, które dla nich nie mają sensu ani wartości ani też praktycznego zastosowania… to naprawdę NIE JEST matematyka. Matematyka to taka potężna szkoła myślenia, tworzenia, testowania, budowania, poszukiwania rozwiązań, strategii, wyciągania wniosków, analizowania oraz oceniania, szacowania i przewidywania… poprzez zadawanie pytań i poszukiwanie odpowiedzi! To naprawdę potężny gmach, prawda?

 

>I właśnie chodzi mi o to, aby inne zagadnienia i treści również realizować w ten sposób. Czas i odpowiednie warunki na to, aby zająć się zadaniami oraz obliczeniami związanymi z twierdzeniem Pitagorasa spokojnie znajdzie się w szkole średniej. Wtedy nie tylko będzie na to właściwy czas, ale zostanie to zrealizowane pięć razy szybciej i dziesięć razy bardziej skutecznie. Efekty będą długotrwałe nie dlatego, że dziecko rozwiąże 50 zadań z danego zagadnienia, tylko dlatego, że będzie w pełni rozumiało sens tego co robi oraz zadania będą odpowiednio dobrane, aby za każdym razem odkrywać i dostrzegać coś nowego, ciekawego i niesamowitego.

 

>Pytajcie kochani i komentujcie, bo chciałbym abyście zrozumieli i uświadomili sobie o czym mówię, gdy podkreślam, że matematyki niestety nie uczymy od lat, ale uczymy rachunków oraz wiecznie przygotowujemy uczniów do egzaminów i testów. Gdybyście chcieli zadać mi pytanie czy ja byłem w szkole uczony matematyki, to po części tak, ale tylko w szkole podstawowej. W szkole średniej to była nauka rachunkowości w oparciu o matematyczne koncepcje. Niestety nie miało to nic wspólnego z PRAWDZIWĄ MATEMATYKĄ o której próbuję wam opowiadać.

 

 

>Marzę o tym, aby absolutnie każdy nauczyciel matematyki mógł wykorzystywać matematykę do tego, aby rozwijać myślenie oraz wszystkie właściwości, które wyżej wspomniałem. Na ten moment stety lub niestety prym wiodą nauczyciele ze szkół niepublicznych oraz nauczyciele przewodnicy, którzy uczą poza systemem. I nie ważne czy nazwiemy ich jako korepetytorzy, specjaliści, pasjonaci, eksperci, profesjonaliści, zawodowcy czy jeszcze inaczej… oni po prostu bardzo mocno odjeżdżają od tego co jest proponowane w szkole systemowej. Dlatego nie dziwmy się później efektom, że nauczyciel pozasystemowy jest w stanie uczyć 2, 3 czy 5 razy lepiej, skuteczniej i skutki są długotrwałe. Oczywiście wiąże się to z wieloma innymi rzeczami z którymi nauczyciele w szkole muszą się mierzyć (jak kto woli – z którymi muszą walczyć, aby przeżyć), ale nie miejmy złudzeń – matematyka w szkole systemowej raczej nie będzie zbyt dobrze realizowana, dopóki nauczyciele nie będą mieli odpowiednich warunków pracy oraz odpowiednio wysokich kompetencji. Bez tego nawet Salomon z pustego nie naleje.

 

>Mam nadzieję, że teraz w pełni rozumiecie dlaczego łapię się za głowę, gdy czytam, że „w końcu będziemy mieli nowoczesną podstawę programową z matematyki”. Ja po prostu kochani zbyt dużo wiem, bo uczę się od najlepszych. To co ja przekazuję to taka forma wołania na puszczy i anegdotycznego „nie strzelajmy do posłańca”.

>Ja doskonale zdaję sobie sprawę jak uczą najlepsi na świecie i na czym opierają swoje mistrzostwo (kompetencje). Po prostu mam na tym punkcie obsesję, więc widząc to co my oferujemy jako edukacja matematyczna, a to co moglibyśmy zaoferować jako jedni z najlepszych na świecie jeśli chodzi o myślenie, olimpiady, międzynarodowe zawody z matematyki, informatyki i innych ścisłych nauk… tak, mamy taki potencjał, że on jest na skalę ŚWIATOWĄ.

 

 

>Tak, my Polacy mamy coś z czego powinniśmy być cholerni dumni i to my powinniśmy być tą „legendarną Finlandią” w kontekście chociażby edukacji matematycznej. Nie muszę chyba wspominać o szkole lwowskiej, gdzie nasze najtęższe umysły i legendarni matematycy pokazywali całemu światu w jaki sposób traktować naukę oraz jak rozwiązywać najtrudniejsze problemy (wyzwania), które cały świat naukowy nie był w stanie bez nas rozgryźć.

 

>Dlatego chciałbym kochani, abyście ZAWSZE pamiętali i mieli to z tyłu głowy, że jak krytykuję to co mamy obecnie w kontekście edukacji matematycznej, to dlatego, że wiem, że stać nas na tysiąc razy więcej. Zawsze powtarzam, że Polacy są w stanie wymyslać oraz rozwiązywać najtrudniejsze problemy i wyzwania na świecie. Dowodami na to są chociażby dziesiątki czy nawet setki naukowców i inżynierów, którzy to realizują od lat, tylko nie zawsze o nich wiemy. Dzięki chociażby Maciejowi Kaweckiemu (kanał This it IT) mogliśmy się ostatnio dowiedzieć o tym jak Mistrz Szubartowski szlifuje diamenty (talenty), których potęgę można zobaczyć chociażby w najbardziej prestiżowych korporacjach (np. OpenAI).

 

 

>Z polskiego na nasz. Jak widzę, że od wielu lat jeździmy na ledwie trzymającym się rowerze, a mam dostęp do tego jak można jeździć samochodami, latać samolotami oraz rakietami, to łapię się za głowę. Nasza edukacja matematyczna przeżywa potężny kryzys, a przecież moglibyśmy być „drugą Finlandią”, gdybyśmy tylko pozwolili ekspertom i pasjonatom oraz naukowcom działać.

 

Mam nadzieję, że dotarliście do końca. Co mam dla was jako materiały dodatkowe? Już wyjaśniam.

 

1)Obrazki (slajdy) w kontekście dowodzenia wizualnego dotyczącego twierdzenia Pitagorasa. Inaczej mówiąc, kilka sposobów na to, aby odpowiednio rozcinać mniejsze kwadraty, aby złożyły się na ten największy. Przy czym, aby lepiej zrozumieć te obrazki, pamiętajcie o tym, że suma pól czerwonych części (pierwotnie tych dwóch mniejszych kwadratów) musi dawać sumę pól niebieskich części (pierwotnie największego kwadratu).

 

2)Film do tego, abyście zobaczyli w jaki sposób składać owe części, aby dawać możliwość dzieciom dowodzenia na ICH POZIOMIE rozwojowym oraz posiadanych kompetencji matematycznych. Trwa niecałą minutę, więc zachęcam do obejrzenia. To jest przysłowiowa matematyczna petarda, więc uprzedzam i ostrzegam, że nie da się tego odzobaczyć. Jak obejrzycie go kilkukrotnie (można także zatrzymywać wiele razy), to nigdy więcej nie pomyślicie o tym, że matematyka to jedynie rachunku albo o tym, że musi być głupia, nudna oraz nieść ze sobą upokorzenie i lęk (tutaj przesyłam mocne przytulenie wirtualne dla Kaśka Szmit)

 

3)Klonowanie i układanie kwadratów, prostokątów i trójkątów dla zaawansowanych – czyli jak przemycić pociągi Sierpińskiego i trójkąty Pitagorasa. Link do artykułu, który opracowałem nieco ponad 3 lata temu, aby pokazać, że matematyka odpowiednio uczona to jest coś czego wiele osób nigdy nie doświadczyło, więc nie jest w stanie wyobrazić sobie jak potężna to siła rozwojowa. Zwłaszcza polecam sam koniec artykułu „CZĘŚĆ 3: Budowanie (układanie) na trójkącie prostokątnym …”, bo w nim macie drobne rozwinięcie tego o czym pisałem w pytaniu nr 9 i 10.

 

4)PRAWDZIWA UCZTA: Link do 122 sposobów dotyczacych udowodnienia twierdzenia Pitagorasa. Nie musicie nawet czytać wszystkiego, lecz powoli przeskrolujcie sobie stronę, patrząc na to jak potężna może być jedna koncepcja matematyczna. To powinno wam „rozwalić mózg/umysł” i uświadomić dobitnie, że myślenie abstrakcyjne i dowodzenie formalne to coś potężnego, ale musi być realizowane dopiero wtedy, gdy dziecko (uczeń) osiągnie dany etap rozwojowy, który temu odpowiada. Możecie w komentarzach napisać, które ze sposobów sprawiły, że szczęka wam o(d)padła!

 

5)Publikacja związana z lękiem przed matematyką. Jest to 61 stron na których zostały przedstawione (omówione) kwestie związane z lękiem przed matematyką jak też metody zmniejszające jego poziom. Wierzę, że to również może być przydatna wiedza zarówno dla nauczycieli matematyki jak i rodziców czy nawet uczniów.

 

 

>Jestem przekonany, że teraz tym pakietem niektórym z was zabiłem przysłowiowego ćwieka. Jestem przekonany, że Lidia Bielinis wraz z Bernadetta Olender-Jermacz będą przyglądały się temu z pełnym niedowierzaniem, a Kaśka Szmit będzie mogła jeszcze lepiej i pełniej dostrzec, że edukacja matematyczna może być przygodą, nauką, odkrywaniem jak też przeżywaniem pozytywnych emocji, na bazie prawidłowo realizowanego procesu edukacyjnego pod kierunkiem (przewodnictwem) odpowiedzialnego nauczyciela

 

Tak na marginesie: mija już niemal 3 lata od momentu, gdy Profesor Roman Leppert zadał mi (oraz Aleksandra Jakubczak wraz z Zuzia Jastrzębska-Krajewska) bardzo trudne pytanie „co dalej z tą matematyką?” i jak widać… te odpowiedzi (zebrane razem) niebawem przerodzą się w rozprawę naukową

 

 

 

 

Źródło: www.facebook.com/tomasz.pintal/